Differences between the modal spectral analysis for non-linear analyses and the modal vibration analysis
Seismic mass computation
In the case of the modal spectral analysis, in order to compute the seismic mass of the structure, the gravity loads acting on the structure in a given non-linear combination are analysed and 100 % of the self-weight and dead load are considered, and the percentage of the use and snow overloads are considered as permanent, which is set in the seismic panel of the program.
For the modal vibration analysis, only loads of a gravity nature involved in the load case under analysis are considered to contribute for mass purposes, and will do so with the combination coefficients of that case.
Direction where the masses are acting
In the modal vibration analysis, for each load case, the direction in which the masses act must be defined. The program offers the following options:
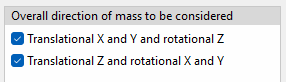
With the first option, the masses act in the global translational X and Y directions, and in rotation about the global Z axis. With the second option, the masses act in the global translational direction Z, and in rotation about the global X and Y axes.
These settings modify the mass matrix, resulting in different modal shapes and frequencies depending on the selection made.
In the modal spectral analysis, the program analyses a model in which mass has been considered in all translational and rotational directions, a situation equivalent to checking both options. Once the modes have been analysed, a filter is applied whereby the program only keeps those modes that mobilise mass according to translational degrees of freedom X and Y and rotational degree of freedom Z. We proceed in this way to achieve an analogy between the linear and the non-linear modal spectral analysis, since in the linear analysis of CYPE 3D the program condenses the degrees of freedom to consider only the translational degrees of freedom X and Y.
Scaling of modal forms
For each mode in the modal vibration analysis, the program represents a scaled modal shape {φ} such that the maximum global displacement of the mode is equal to 1:
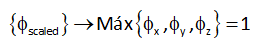
In modal spectral analysis, for each seismic load considered, the modal shape is multiplied by a mode factor so that the modal deformation is:
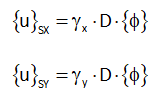
Where:
γi: modal share factor in the “i” direction:
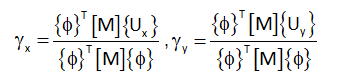
Where {Ux} and {Uy} are vectors, of dimension equal to the GDL of the dynamic model, with all their components null except those according to the degrees of freedom in the translational direction X and Y respectively, which will be equal to unity, and [M] is the mass matrix.
D: spectral shift of the mode
D = A/ω2, where
A: spectral acceleration of the mode
ω = 2π/T, where T is the period of the mode
{φ}: modal form (autovector)
These elastic deformations, {u}SX and {u}SY, shall be multiplied by the corresponding ductility or displacement factor to consider the inelastic displacement.


